Модель. Математический Маятник
Однако изучать механизмы действия маятника эффективнее всего именно на упрощенной модели — на примере математического маятника. Математический маятник. Интерактивная модель математического маятника.
3.7 Колебания математического маятника Колебательное движение - одно из самых распространенных в природе. Разнообразные маятники в часах и других технических устройствах, колебания мембран и оболочек, колебания атомов в молекулах, ионов и молекул в кристаллах и многие другие процессы в живой и неживой природе в чем-то схожи: объект движется таким образом, что многократно проходит через одни и те же точки, периодически воспроизводя одно и то же состояние. Изучив его движение на сравнительно коротком отрезке времени, включающем один период, мы можем составить полное представление о его движении в будущем (если оно не будет изменено вмешательством извне). Хотя колебательные движения бывают весьма многообразны, их сущность можно постичь на нескольких относительно простых примерах. Остановимся на одном из самых простых, название которого вынесено в заголовок. Этот пример рассматривается в любом школьном курсе физики, но, располагая более совершенным математическим аппаратом и прибегая к компьютерному моделированию, можно продвинуться в изучении колебаний математического маятника дальше и понять закономерности колебательного движения глубже. Рассмотрим идеализированную систему, состоящую из тела массы т, прикрепленного к нижнему концу жесткого «невесомого» стержня длиной l, верхний конец которого вращается без трения в точке подвеса, рисунке 3.7.1.
Если груз отклонить от положения равновесия на угол θ 0 и отпустить, то «математический маятник» будет колебаться в вертикальной плоскости. Рисунок 3.7.1 – Колебания математического маятника Поскольку движение груза происходит по дуге окружности радиуса l, то его положение характеризуется в каждое мгновение углом θ.
Линейная скорость и ускорение равны (3.7.1) На груз действуют две силы: сила тяжести и упругая сила натяжения стержня. При выводе уравнения движения достаточно учесть лишь компоненту силы, направленную по касательной к дуге: F = mg s i n θ, направлена она в сторону уменьшения θ.
Сила перпендикулярна к касательной и вклада в это уравнение не дает. Уравнение движения примет вид (3.7.2) Обычно в курсе физики ограничиваются исследованием малых колебаний.
Модель 'Математический маятник' демонстрирует свободные колебания математического маятника. Можно изменять длину нити l, угол начального отклонения маятника, коэффициент вязкого трения b.
Выводятся графики зависимости от времени угловой координаты и скорости, диаграммы потенциальной и кинетической энергий при свободных колебаниях, а также при затухающих колебаниях при наличии вязкого трения. Слайд 8 из презентации «Моделирование в электронных таблицах» Размеры: 720 х 540 пикселей, формат:.jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как.». Скачать всю презентацию «Моделирование в электронных таблицах.ppt» можно в zip-архиве размером 1863 КБ. Скачать презентацию.
Краткое содержание других презентаций на тему слайда - Разновидности звука. Применение инфразвука имеет большое значение в военном деле. Распространение и приемники звука. Ультразвуком пользуются летучие мыши при охоте в ночное время. Скорость - Зависит от среды и температуры. Звуковые волны. Звук «До» (рис.2), но более жестко.
Высота - Определяется частотой колебаний, от 15 до20 000 Гц. Звуковые колебания. Гармонические колебания. Положение системы задаётся углом отклонения.
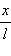
Лекции по физике. Малые колебания.
Сложение колебаний. Явление резонанса. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно.
Математический маятник. При f(t)=F0?cos(??t) решение уравнения (1) имеет вид: - Т = t/N t - время всех колебаний N - число колебаний. Вертикальный пружинный маятник. Явление распространения колебаний в пространстве с течением времени называется волной. M – масса тела (кг) k – жесткость пружины (Н/м). Механические колебания Волны.
Скорость волны. L – длина маятника (м), g – ускорение свободного падения (м/с2). Драйвер для сопроцессора windows 7. Модулированными.
Колебания синфазны. Аналитический: Вращающийся вектор амплитуды полностью характеризует гармоническое колебание. Начальные фазы колебаний одинаковы. Колебания вида. По правилу сложения векторов найдем суммарную амплитуду, результирующего колебания: 3. Разность фаз изменяется во времени произвольным образом. На рисунке изображена укрепленная в тисках упругая металлическая линейка.
Карты железных дорог россии. Приятной поездки по красивым просторам необъятной страны! Увеличивайте, двигайте ее для нахождения нужного вам региона, пользуйтесь кнопками зума в правом нижнем углу окна.
Звук камертона является чистым тоном. Что же такое звуковые колебания? В данном случае колебания источника звука очевидны. Звук распространяется во всех упругих телах, но не может распространяться в безвоздушном пространстве.
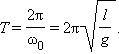
Интерактивная Модель Математического Маятника Онлайн

Громкость звука. Единица измерения (метр м). Кол – во часов.
Частота колебаний? - число полных колебаний, совершаемых телом за единицу времени.
Физическая Модель Математического Маятника
«Мир, в котором мы живем, удивительно склонен к колебаниям» Р. Основные характеристики колебательного процесса (движения). Собственная циклическая частота колебаний математического маятника на некоторой планете 5 рад/с.